베이즈 이론 정리

베이즈 정리란

두 확률 변수의 사전 확률과 사후 확률 사이의 관계를 나타내는 정리이다.

베이즈 확률론 해석에 따르면 베이즈 정리는 사전 확률로부터 사후확률을 구할 수 있다.

베이즈 정리 - 위키백과, 우리 모두의 백과사전

위에서 말한 의미를 정확하게 이해할 수는 없지만 사전확률, 사후확률 두개의 키워드를 가지고가면 좋겠다.

 

사전확률(prior probability) : 특정 사건이 일어나기 전의 확률

- 현재 가지고 있는 정보를 기초로 하여 정한 확률

- 주사위를 굴렸을때 1이 나올 확률, 동전을 던졌을 때 앞면이 나올 확률 등..

 

사후확률(posteriori probability) : 사건이 발생 후에 어떤 원인으로부터 일어난 것이라고 보는 확률

- 추가된 정보로부터 사전 정보를 업데이트한 확률

 

베이즈 이론에 사용된 조건부 확률부터 알아보겠다.

조건부 확률의 식은 아래와 같다.

$$P(A|B)=\frac{P(A\cap B)}{P(B)}$$

 

식으로만 보기에는 어려움이 있어 그림과 함께 보는것을 추천한다.

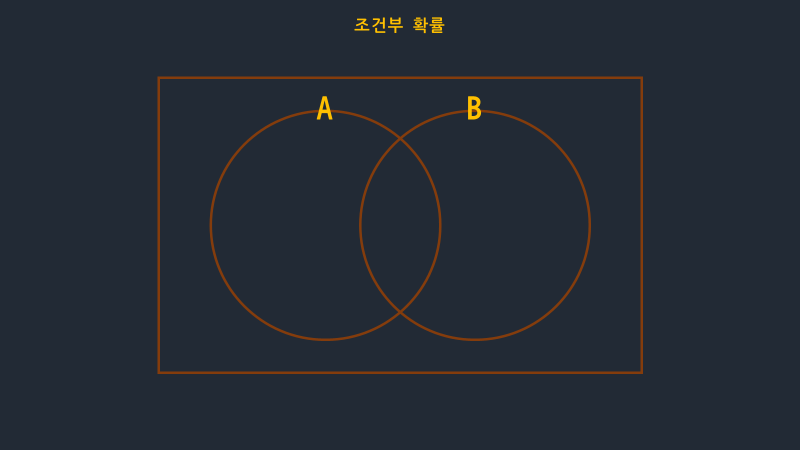
A와 B를 둘러싸고 있는 사각형은 어떤 확률 공간이고, 그 확률 공간안에는 왼쪽 원(A), 오른쪽 원(B)가 있다.

그림과 같이 색칠된 부분을 P(A)라고 하고,

그림과 같은 부분을 P(B)라고 한다.

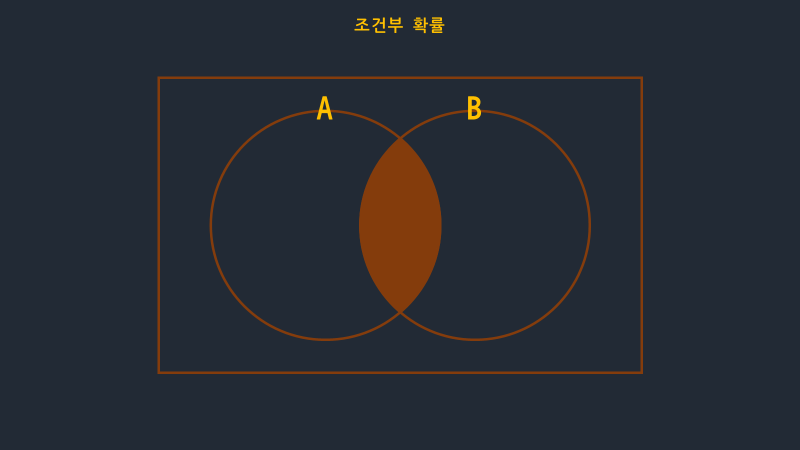
이것은 

$$ P(A\cap B) $$ A와 B의 교집합을 의미한다.

 

조건부 확률의 식

$$P(A|B)=\frac{P(A\cap B)}{P(B)}$$

의 의미는 아래의 그림과 같다.

위의 식에서 양변에 P(B)를 곱하면

$$P(A|B)P(B)=P(A\cap B))$$

가 되고 이것은 베이즈 정리에 사용된다.

정리를 해보자면 P(B)가 일어났을때 A의 확률 P(A)는 A와 B의 교집합으로 알 수 있다.

 

베이즈 이론(Bayes Theorem)

위에서 보았듯이 

$$P(A|B)=\frac{P(A\cap B)}{P(B)}$$

라면

$$P(B|A)=\frac{P(B\cap A)}{P(A)}$$

가 될것이다. 

A와 B의 교집합은 B와 A의 교집합과 같다. 이를 수식으로 표현하면

$$P(A\cap B) = P(B\cap A)$$

위와 같이 되며, 위에서 알아보았던 조건부 확률을 정리한 것을 사용하게 되면

$$P(A|B)\cdot P(B)=P(B|A)\cdot P(A)$$

따라서

$$P(A|B)=\frac{P(B|A)\cdot P(A)}{P(B)}$$

로 정리할 수 있다.

우리가 기억해두었던 키워드를 대입해보면

P(A|B) : 사후 확률(B라는 정보가 업데이트 된 이후의 확률)

P(A) : 사전 확률(B라는 정보가 업데이트 되기전에 우리가 알고있는 정보를 기초로한 확률)

로 표현 할 수 있다.

 

베이즈 정리를 이론만 본다면 이해가 잘되지 않기 때문에 간단예제를 가져와 보았다.

우리가 범인을 예측하는 상황 가정할 때

내 앞에 있는 용의자가 50%정도로 범인이라고 확신하고 있다.

범인이 장발이라는 중요한 정보가 들어왔고 이것의 확률은 80%라고 하자.

또한 범인이 아닌 사람들이 장발일 경우에는 30%라고 한다.

만약 내 앞에 있는 사람(용의자)이 장발일 때 범인이라고 얼마나 확신할 수 있는가?

 

문제가 조금 이해가 안될 수 있지만 여기서 필요한 키워드만 빼 보았다.

우리가 구해야 하는 값의 식은 아래와 같다.

$$P(A|B)=\frac{P(B|A)\cdot P(A)}{P(B)}$$

 

나머지는 위의 키워드에 나와있지만 P(B) 나와있지 않다.

P(B)를 구하는 공식을 아래와 같다.

$$P(B) = P(B|A)\cdot P(B) + P(B|A^{c})\cdot P(A^{c})$$

P(B)를 구하는 공식을 말로 풀어서 이야기하자면 범인일때와 범인이아닐때(A사건일때 A사건이 아닐때)의 B의 확률이다.

즉 모든상황에서의 B의 확률이라고 이야기할 수 있겠다.

 

식을 정리한다면 아래와 같이 나올것이다.

$$\frac{P(B|A)\cdot P(A)}{P(B|A)\cdot P(B) + P(B|A^{c})\cdot P(A^{c})}$$

위에서 구한 값들을 구해서 대입한다면 

$$\frac{0.8\times 0.5}{(0.8\times 0.5)+(0.3\times 0.5)}$$

값을 구하면

$$P(A|B)= 72\%$$

가 나오게된다.

def solve(criminal, criminal_long_hair, not_criminal_long_hair):
  #분자부분
  numerator = criminal_long_hair * criminal
  #분모부분
  denominator = (criminal_long_hair *criminal) + (not_criminal_long_hair * (1-criminal))
  ans = numerator / denominator
  return ans
  
criminal = 0.5
criminal_long_hair = 0.8
not_criminal_long_hair = 0.3
solve(criminal, criminal_long_hair, not_criminal_long_hair)

마지막으로 파이썬 코드로 정리하였다.